投稿者: 山野ごんた

【授業観察】アクティブ・ラーニングは一日にしてならず

先日，元筑波附属小学校副校長の細水保宏先生の授業を見る機会がありました。以前にも，先生の授業を参観させていただいたことがあります。その時の授業では，授業者としてのスキルの一つ一つ高さに驚いたのものです。今回の授業でもたくさんの学ぶべきものをいただくことができました。 “【授業観察】アクティブ・ラーニングは一日にしてならず” の続きを読む

【AL指導案】算数　1年　ひきざん　（減加法と減減法）

平成27年度の指導案です。とあるサークルで授業公開したもので，プレ授業もしていただけるという事で，どんな声がけを想定しているかが後ろについています。授業の雰囲気をつかんでいただくには，実はこっちのほうが良いかと思い，2本目の指導案に選びました。

場合による減加法，減減法の優位性などは，算数教師には格好の題材のように感じます。ですが，1年生のこの段階では，どの教科書会社でも扱っておらず，指導要領を読む限りでも「発展的な内容」として扱うほかはないようです。そこで，並列する形での授業づくりを心がけました。

ひきざん　減加法と減減法　指導案

【実践】ワールドカフェ【後編】

記事が長くなったので切っていた前編でした。すっかり忘れて別な記事を書いていましたが，最近の閲覧履歴を見ると，結構前篇を読んでくださっている方が多い！ということで，急いで後編を書きます。 “【実践】ワールドカフェ【後編】” の続きを読む

【AL指導案】算数　2年　たし算のしかたを考えよう　（交換法則）

平成28年度4月現在の指導案です。一応3つの柱を受けて「資質・能力」についても書いています。ただ（仮）となっているように，適切に使われるためには，ワーキンググループの資料などを通して，どんどん修正が必要かと思います。

また，単元計画の一部が無くなってしまっています。ご了承ください。

算数2年指導案　たし算のしかたを考えよう

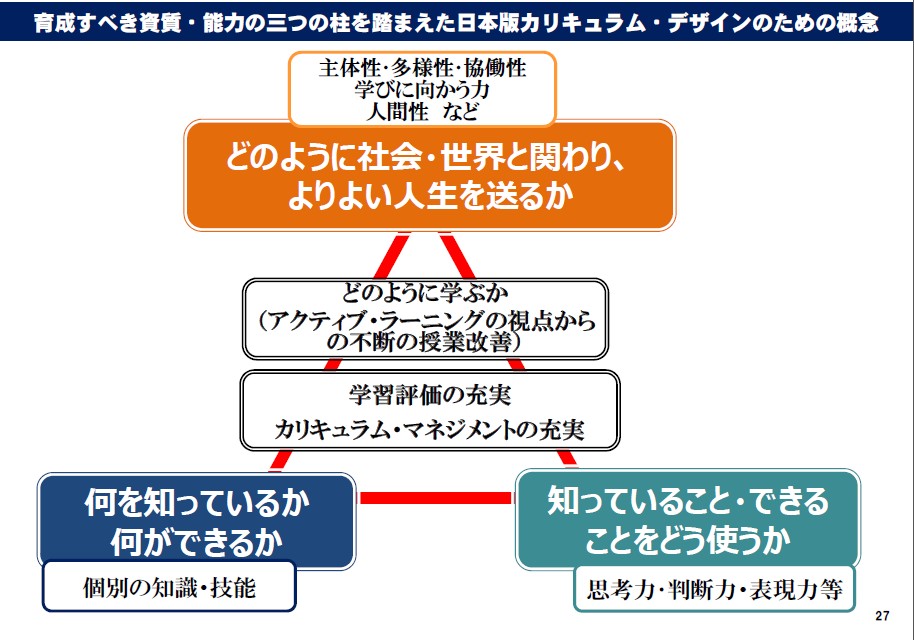
【論点整理】育成すべき資質・能力　「3つの柱」

文部科学省では各教科等において，

「初等中等教育における教育課程の基準等の在り方について（諮問）」を受け、その基本的方向性に関する論点整理を踏まえ、学習指導要領全体が目指す姿を念頭に置きつつ、
各学校段階又は各教科・科目等の改訂の方向性について専門的に検討するため

ワーキンググループ資料「学校段階等別部会及び教科等別ワーキンググループ等の 設置について」より

以上の理由により，それぞれのワーキンググループを設置してその会議の資料を公開しています。日々更新されているので，一通り目を通したいところですが，全教科等となるとあまりに資料が多いので，視点を絞って見ることをお勧めします。難しい話も多いですが…。
リンクはこちらから辿ると良いと思います。 “【論点整理】育成すべき資質・能力　「3つの柱」” の続きを読む

ALにおける振り返りの在り方

6月4日に行われたNew Education Expo 2016に参加させていただき，文部科学省の田村先生のお話を聞くことができました。参考になる話はたくさんあったのですが，特に振り返りに特化して，また最近考えていることを交えながら，紹介していこうと思います。 “ALにおける振り返りの在り方” の続きを読む

特集　アクティブ・ラーニングを妨げるもの　を読んで

筑波大学附属小学校算数研究部から出ている「算数授業研究」という本があるのですが，表題のテーマで出版されていました。2016年冬号（102号）です。

面白い記述がたくさんあったので，抜粋で紹介してみたいと思います。 “特集　アクティブ・ラーニングを妨げるもの　を読んで” の続きを読む

算数科のアクティブ・ラーニングの定義はここにある！

算数科の教科調査官，笠井健一先生が書かれています。

前半部にアクティブ・ラーニングで大切にしてほしい事。
後半部は，アクティブ・ラーニングと言える各小学校の実践が載っています。

前半部は結構はっきりとした切り口で，例えば

問題解決型の学習であっても，教師主導の授業展開では，主体的に学んでいるとは言えない。

といったことが書かれており，未だ「問題解決型学習⇒AL」と捉えている人も少なくない現状においては，なかなか衝撃的な内容と言えるのではないでしょうか。

 

後半の実践は，笠井先生が授業を見られたり，研究に関わっている学校の先生方が寄稿した，それぞれの学校の研究の取組です。

いい意味で尖った実践が多くて，非常に面白いです。カテゴリ（主体・協働・ICT・複式など）で分けられており，それぞれの学校の取組が，共通の視点で説明されています。

個人的には，学び合いをしている学校の「個人解決」は5分程度のものが多いところが面白いなと感じました。